Adsorption Energies in MOFs

Pre-trained ODAC models are versatile across various MOF-related tasks. To begin, we’ll start with a fundamental application: calculating the adsorption energy for a single CO₂ molecule. This serves as an excellent and simple demonstration of what you can achieve with these datasets and models.

For predicting the adsorption energy of a single CO₂ molecule within a MOF structure, the adsorption energy ( $E_{\mathrm{ads}}$ ) is defined as:

E_{\mathrm{ads}} = E_{\mathrm{MOF+CO2}} - E_{\mathrm{MOF}} - E_{\mathrm{CO2}} \tag{1}

(1)

Each term on the right-hand side represents the energy of the relaxed state of the indicated chemical system. For a comprehensive understanding of our methodology for computing these adsorption energies, please refer to our paper.

Loading Pre-trained Models¶

Need to install fairchem-core or get UMA access or getting permissions/401 errors?

Install the necessary packages using pip, uv etc

! pip install fairchem-core fairchem-data-oc fairchem-applications-cattsunami

Get access to any necessary huggingface gated models
- Get and login to your Huggingface account
- Request access to https://huggingface.co/facebook/UMA
- Create a Huggingface token at https://huggingface.co/settings/tokens/ with the permission “Permissions: Read access to contents of all public gated repos you can access”
- Add the token as an environment variable using huggingface-cli login or by setting the HF_TOKEN environment variable.

# Login using the huggingface-cli utility
! huggingface-cli login

# alternatively,
import os
os.environ['HF_TOKEN'] = 'MY_TOKEN'

A pre-trained model can be loaded using FAIRChemCalculator. In this example, we’ll employ UMA to determine the CO₂ adsorption energies.

from fairchem.core import FAIRChemCalculator, pretrained_mlip

predictor = pretrained_mlip.get_predict_unit("uma-s-1p1")
calc = FAIRChemCalculator(predictor, task_name="odac")

WARNING:root:device was not explicitly set, using device='cuda'.

WARNING:root:If 'dataset_list' is provided in the config, the code assumes that each dataset maps to itself. Please use 'dataset_mapping' as 'dataset_list' is deprecated and will be removed in the future.

Adsorption in rigid MOFs: CO₂ Adsorption Energy in Mg-MOF-74¶

Let’s apply our knowledge to Mg-MOF-74, a widely studied MOF known for its excellent CO₂ adsorption properties. Its structure comprises magnesium atomic complexes connected by a carboxylated and oxidized benzene ring, serving as an organic linker. Previous studies consistently report the CO₂ adsorption energy for Mg-MOF-74 to be around -0.40 eV [1] [2] [3].

Our goal is to verify if we can achieve a similar value by performing a simple single-point calculation using UMA. In the ODAC23 dataset, all MOF structures are identified by their CSD (Cambridge Structural Database) code. For Mg-MOF-74, this code is OPAGIX. We’ve extracted a specific OPAGIX+CO2 configuration from the dataset, which exhibits the lowest adsorption energy among its counterparts.

import matplotlib.pyplot as plt
from ase.io import read
from ase.visualize.plot import plot_atoms

mof_co2 = read("structures/OPAGIX_w_CO2.cif")
mof = read("structures/OPAGIX.cif")
co2 = read("structures/co2.xyz")

fig, ax = plt.subplots(figsize=(5, 4.5), dpi=250)
plot_atoms(mof_co2, ax)
ax.set_axis_off()

The final step in calculating the adsorption energy involves connecting the FAIRChemCalculator to each relaxed structure: OPAGIX+CO2, OPAGIX, and CO2. The structures used here are already relaxed from ODAC23. For simplicity, we assume here that further relaxations can be neglected. We will show how to go beyond this assumption in the next section.

mof_co2.calc = calc
mof.calc = calc
co2.calc = calc

E_ads = (
    mof_co2.get_potential_energy()
    - mof.get_potential_energy()
    - co2.get_potential_energy()
)

print(f"Adsorption energy of CO2 in Mg-MOF-74: {E_ads:.3f} eV")

Adsorption energy of CO2 in Mg-MOF-74: -0.459 eV

Adsorption in flexible MOFs¶

The adsorption energy calculation method outlined above is typically performed with rigid MOFs for simplicity. Both experimental and modeling literature have shown, however, that MOF flexibility can be important in accurately capturing the underlying chemistry of adsorption [1] [2] [3]. In particular, uptake can be improved by treating MOFs as flexible. Two types of MOF flexibility can be considered: intrinsic flexibility and deformation induced by guest molecules. In the Open DAC Project, we consider the latter MOF deformation by allowing the atomic positions of the MOF to relax during geometry optimization [4]. The addition of additional degrees of freedoms can complicate the computation of the adsorption energy and necessitates an extra step in the calculation procedure.

The figure below shows water adsorption in the MOF with CSD code WOBHEB with added defects (WOBHEB_0.11_0) from a DFT simulation. A typical adsorption energy calculation would only seek to capture the effects shaded in purple, which include both chemisorption and non-bonded interactions between the host and guest molecule. When allowing the MOF to relax, however, the adsorption energy also includes the energetic effect of the MOF deformation highlighted in green.

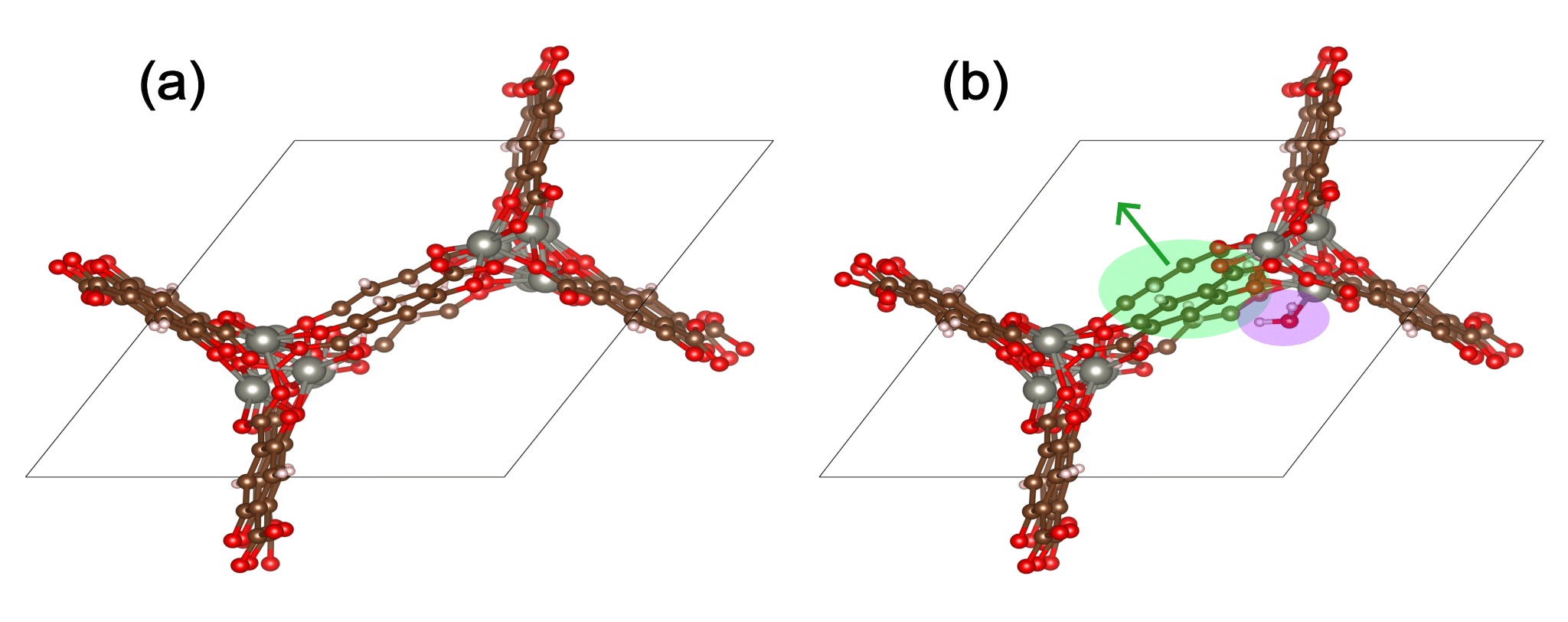
To account for this deformation, it is vital to use the most energetically favorable MOF geometry for the empty MOF term in Eqn. 1. Including MOF atomic coordinates as degrees of freedom can result in three possible outcomes:

The MOF does not deform, so the energies of the relaxed empty MOF and the MOF in the adsorbed state are the same
The MOF deforms to a less energetically favorable geometry than its ground state
The MOF locates a new energetically favorable geoemtry relative to the empty MOF relaxation

The first outcome requires no additional computation because the MOF rigidity assumption is valid. The second outcome represents physical and reversible deformation where the MOF returns to its empty ground state upon removal of the guest molecule. The third outcome is often the result of the guest molecule breaking local symmetry. We also found cases in ODAC in which both outcomes 2 and 3 occur within the same MOF.

To ensure the most energetically favorable empty MOF geometry is found, an addition empty MOF relaxation should be performed after MOF + adsorbate relaxation. The guest molecule should be removed, and the MOF should be relaxed starting from its geometry in the adsorbed state. If all deformation is reversible, the MOF will return to its original empty geometry. Otherwise, the lowest energy (most favorable) MOF geometry should be taken as the reference energy, $E_{\mathrm{MOF}}$ , in Eqn. 1.

H₂O Adsorption Energy in Flexible WOBHEB with UMA¶

The first part of this tutorial demonstrates how to perform a single point adsorption energy calculation using UMA. To treat MOFs as flexible, we perform all calculations on geometries determined by geometry optimization. The following example corresponds to the figure shown above (H₂O adsorption in WOBHEB_0.11_0).

In this tutorial, $E_{x}(r_{y})$ corresponds to the energy of $x$ determined from geometry optimization of $y$ .

First, we obtain the energy of the empty MOF from relaxation of only the MOF: $E_{\mathrm{MOF}}(r_{\mathrm{MOF}})$

import ase.io
from ase.optimize import BFGS

mof = ase.io.read("structures/WOBHEB_0.11.cif")
mof.calc = calc
relax = BFGS(mof)
relax.run(fmax=0.05)
E_mof_empty = mof.get_potential_energy()
print(f"Energy of empty MOF: {E_mof_empty:.3f} eV")

      Step     Time          Energy          fmax
BFGS:    0 23:05:08    -1077.274065        0.206406

BFGS:    1 23:05:09    -1077.276780        0.152729

BFGS:    2 23:05:10    -1077.281942        0.169926

BFGS:    3 23:05:11    -1077.284771        0.155763

BFGS:    4 23:05:11    -1077.288834        0.108771

BFGS:    5 23:05:11    -1077.291023        0.086446

BFGS:    6 23:05:12    -1077.293362        0.093448

BFGS:    7 23:05:13    -1077.295414        0.100138

BFGS:    8 23:05:13    -1077.297829        0.102535

BFGS:    9 23:05:15    -1077.300013        0.091603

BFGS:   10 23:05:17    -1077.302011        0.078958

BFGS:   11 23:05:17    -1077.304137        0.105563

BFGS:   12 23:05:17    -1077.306724        0.087907

BFGS:   13 23:05:18    -1077.309517        0.086364

BFGS:   14 23:05:18    -1077.312263        0.086863

BFGS:   15 23:05:19    -1077.314701        0.106278

BFGS:   16 23:05:19    -1077.316986        0.106217

BFGS:   17 23:05:20    -1077.319484        0.085427

BFGS:   18 23:05:20    -1077.322263        0.109640

BFGS:   19 23:05:21    -1077.325135        0.148669

BFGS:   20 23:05:21    -1077.327766        0.125926

BFGS:   21 23:05:23    -1077.329920        0.069120

BFGS:   22 23:05:25    -1077.331952        0.087277

BFGS:   23 23:05:26    -1077.334273        0.125237

BFGS:   24 23:05:27    -1077.336835        0.166696

BFGS:   25 23:05:27    -1077.339543        0.145540

BFGS:   26 23:05:28    -1077.342148        0.087640

BFGS:   27 23:05:28    -1077.344542        0.076211

BFGS:   28 23:05:29    -1077.346893        0.148940

BFGS:   29 23:05:29    -1077.349784        0.170253

BFGS:   30 23:05:29    -1077.352529        0.109272

BFGS:   31 23:05:30    -1077.354751        0.070349

BFGS:   32 23:05:30    -1077.356778        0.089705

BFGS:   33 23:05:30    -1077.358657        0.124280

BFGS:   34 23:05:31    -1077.360597        0.108072

BFGS:   35 23:05:32    -1077.362471        0.068554

BFGS:   36 23:05:32    -1077.364166        0.070187

BFGS:   37 23:05:32    -1077.365712        0.105459

BFGS:   38 23:05:33    -1077.367257        0.104161

BFGS:   39 23:05:33    -1077.368767        0.063019

BFGS:   40 23:05:36    -1077.370140        0.058367

BFGS:   41 23:05:39    -1077.371383        0.058770

BFGS:   42 23:05:41    -1077.372482        0.063346

BFGS:   43 23:05:41    -1077.373506        0.055382

BFGS:   44 23:05:42    -1077.374498        0.042291
Energy of empty MOF: -1077.374 eV

Next, we add the H₂O guest molecule and relax the MOF + adsorbate to obtain $E_{\mathrm{MOF+H2O}}(r_{\mathrm{MOF+H2O}})$ .

mof_h2o = ase.io.read("structures/WOBHEB_H2O.cif")
mof_h2o.calc = calc
relax = BFGS(mof_h2o)
relax.run(fmax=0.05)
E_combo = mof_h2o.get_potential_energy()
print(f"Energy of MOF + H2O: {E_combo:.3f} eV")

      Step     Time          Energy          fmax
BFGS:    0 23:05:42    -1091.565588        1.145036

BFGS:    1 23:05:43    -1091.585064        0.314149

BFGS:    2 23:05:43    -1091.590212        0.243429

BFGS:    3 23:05:43    -1091.608167        0.237259

BFGS:    4 23:05:44    -1091.614633        0.227909

BFGS:    5 23:05:44    -1091.625216        0.186828

BFGS:    6 23:05:45    -1091.632353        0.178927

BFGS:    7 23:05:47    -1091.640624        0.175072

BFGS:    8 23:05:47    -1091.648039        0.184491

BFGS:    9 23:05:47    -1091.656144        0.160958

BFGS:   10 23:05:48    -1091.663841        0.178406

BFGS:   11 23:05:48    -1091.672297        0.188726

BFGS:   12 23:05:48    -1091.682087        0.157487

BFGS:   13 23:05:49    -1091.692978        0.177282

BFGS:   14 23:05:49    -1091.704433        0.158175

BFGS:   15 23:05:50    -1091.715510        0.191790

BFGS:   16 23:05:50    -1091.725708        0.197778

BFGS:   17 23:05:50    -1091.735325        0.163735

BFGS:   18 23:05:51    -1091.745537        0.151535

BFGS:   19 23:05:51    -1091.754020        0.170889

BFGS:   20 23:05:51    -1091.761492        0.153765

BFGS:   21 23:05:51    -1091.767890        0.152302

BFGS:   22 23:05:53    -1091.774202        0.165875

BFGS:   23 23:05:54    -1091.780888        0.135516

BFGS:   24 23:05:54    -1091.788351        0.181080

BFGS:   25 23:05:54    -1091.794280        0.204584

BFGS:   26 23:05:55    -1091.800636        0.131359

BFGS:   27 23:05:55    -1091.806517        0.189556

BFGS:   28 23:05:55    -1091.812306        0.199112

BFGS:   29 23:05:56    -1091.817179        0.151644

BFGS:   30 23:05:56    -1091.822212        0.100162

BFGS:   31 23:05:56    -1091.826296        0.125746

BFGS:   32 23:05:58    -1091.832529        0.177403

BFGS:   33 23:06:00    -1091.837115        0.246717

BFGS:   34 23:06:01    -1091.842047        0.112437

BFGS:   35 23:06:01    -1091.845780        0.328522

BFGS:   36 23:06:03    -1091.850877        0.173979

BFGS:   37 23:06:04    -1091.858477        0.159966

BFGS:   38 23:06:05    -1091.865287        0.141074

BFGS:   39 23:06:05    -1091.872005        0.142507

BFGS:   40 23:06:05    -1091.878354        0.242183

BFGS:   41 23:06:06    -1091.881268        0.524486

BFGS:   42 23:06:06    -1091.884787        0.733810

BFGS:   43 23:06:06    -1091.893713        0.205201

BFGS:   44 23:06:07    -1091.898874        0.154866

BFGS:   45 23:06:07    -1091.917403        0.317381

BFGS:   46 23:06:09    -1091.925001        0.327346

BFGS:   47 23:06:09    -1091.943632        0.232350

BFGS:   48 23:06:10    -1091.959187        0.458501

BFGS:   49 23:06:10    -1091.965186        1.155130

BFGS:   50 23:06:11    -1091.964980        1.463737

BFGS:   51 23:06:11    -1092.005735        0.559884

BFGS:   52 23:06:12    -1092.021118        0.289973

BFGS:   53 23:06:12    -1092.063491        0.335282

BFGS:   54 23:06:13    -1092.082404        0.325419

BFGS:   55 23:06:13    -1092.104882        0.607129

BFGS:   56 23:06:15    -1092.121690        0.229615

BFGS:   57 23:06:16    -1092.138181        0.229395

BFGS:   58 23:06:16    -1092.150540        0.188631

BFGS:   59 23:06:16    -1092.164646        0.276043

BFGS:   60 23:06:16    -1092.177335        0.433006

BFGS:   61 23:06:17    -1092.188076        0.446372

BFGS:   62 23:06:17    -1092.198851        0.340839

BFGS:   63 23:06:17    -1092.209976        0.189507

BFGS:   64 23:06:18    -1092.221014        0.140018

BFGS:   65 23:06:18    -1092.229585        0.155958

BFGS:   66 23:06:18    -1092.235876        0.120796

BFGS:   67 23:06:19    -1092.241382        0.097202

BFGS:   68 23:06:19    -1092.247013        0.124405

BFGS:   69 23:06:20    -1092.252422        0.168117

BFGS:   70 23:06:20    -1092.257364        0.155581

BFGS:   71 23:06:20    -1092.262424        0.123190

BFGS:   72 23:06:21    -1092.266808        0.153426

BFGS:   73 23:06:22    -1092.270517        0.176623

BFGS:   74 23:06:23    -1092.274072        0.168299

BFGS:   75 23:06:24    -1092.277533        0.117553

BFGS:   76 23:06:24    -1092.280814        0.081266

BFGS:   77 23:06:25    -1092.284107        0.088314

BFGS:   78 23:06:27    -1092.286626        0.105022

BFGS:   79 23:06:28    -1092.289067        0.090483

BFGS:   80 23:06:28    -1092.291300        0.065899

BFGS:   81 23:06:29    -1092.293091        0.076137

BFGS:   82 23:06:31    -1092.294691        0.080392

BFGS:   83 23:06:31    -1092.296042        0.094850

BFGS:   84 23:06:32    -1092.297503        0.090991

BFGS:   85 23:06:32    -1092.298942        0.097425

BFGS:   86 23:06:32    -1092.300668        0.084134

BFGS:   87 23:06:33    -1092.302339        0.063826

BFGS:   88 23:06:33    -1092.304097        0.053615

BFGS:   89 23:06:33    -1092.305796        0.055280

BFGS:   90 23:06:35    -1092.307151        0.054058

BFGS:   91 23:06:35    -1092.308452        0.048034
Energy of MOF + H2O: -1092.308 eV

We can now isolate the MOF atoms from the relaxed MOF + H₂O geometry and see that the MOF has adopted a geometry that is less energetically favorable than the empty MOF by ~0.2 eV. The energy of the MOF in the adsorbed state corresponds to $E_{\mathrm{MOF}}(r_{\mathrm{MOF+H2O}})$ .

mof_adsorbed_state = mof_h2o[:-3]
mof_adsorbed_state.calc = calc
E_mof_adsorbed_state = mof_adsorbed_state.get_potential_energy()
print(f"Energy of MOF in the adsorbed state: {E_mof_adsorbed_state:.3f} eV")

Energy of MOF in the adsorbed state: -1077.091 eV

H₂O adsorption in this MOF appears to correspond to Case #2 as outlined above. We can now perform re-relaxation of the empty MOF starting from the $r_{\mathrm{MOF+H2O}}$ geometry.

relax = BFGS(mof_adsorbed_state)
relax.run(fmax=0.05)
E_mof_rerelax = mof_adsorbed_state.get_potential_energy()
print(f"Energy of re-relaxed empty MOF: {E_mof_rerelax:.3f} eV")

      Step     Time          Energy          fmax
BFGS:    0 23:06:36    -1077.091356        0.982171

BFGS:    1 23:06:36    -1077.123575        0.870930

BFGS:    2 23:06:36    -1077.172816        0.806666

BFGS:    3 23:06:37    -1077.212851        0.502350

BFGS:    4 23:06:37    -1077.232427        0.440263

BFGS:    5 23:06:39    -1077.249954        0.284640

BFGS:    6 23:06:39    -1077.260700        0.260798

BFGS:    7 23:06:40    -1077.270187        0.247485

BFGS:    8 23:06:40    -1077.279525        0.211762

BFGS:    9 23:06:41    -1077.286456        0.178535

BFGS:   10 23:06:41    -1077.291571        0.149031

BFGS:   11 23:06:43    -1077.295635        0.139213

BFGS:   12 23:06:43    -1077.299260        0.145840

BFGS:   13 23:06:44    -1077.303894        0.182732

BFGS:   14 23:06:46    -1077.308574        0.171438

BFGS:   15 23:06:46    -1077.313120        0.134348

BFGS:   16 23:06:47    -1077.317226        0.165142

BFGS:   17 23:06:47    -1077.321450        0.150408

BFGS:   18 23:06:48    -1077.325841        0.145401

BFGS:   19 23:06:48    -1077.329411        0.114699

BFGS:   20 23:06:48    -1077.332035        0.108752

BFGS:   21 23:06:48    -1077.334287        0.101454

BFGS:   22 23:06:50    -1077.336599        0.123644

BFGS:   23 23:06:51    -1077.339326        0.119983

BFGS:   24 23:06:53    -1077.341968        0.088932

BFGS:   25 23:06:53    -1077.344302        0.091589

BFGS:   26 23:06:55    -1077.346225        0.068003

BFGS:   27 23:06:55    -1077.347774        0.068608

BFGS:   28 23:06:58    -1077.349486        0.090820

BFGS:   29 23:07:01    -1077.351045        0.096652

BFGS:   30 23:07:05    -1077.352657        0.063820

BFGS:   31 23:07:05    -1077.353839        0.050151

BFGS:   32 23:07:05    -1077.355144        0.054063

BFGS:   33 23:07:06    -1077.356513        0.085249

BFGS:   34 23:07:06    -1077.357918        0.079802

BFGS:   35 23:07:06    -1077.359456        0.069575

BFGS:   36 23:07:07    -1077.360867        0.071534

BFGS:   37 23:07:07    -1077.362149        0.073259

BFGS:   38 23:07:08    -1077.363339        0.084855

BFGS:   39 23:07:08    -1077.364672        0.080591

BFGS:   40 23:07:09    -1077.365666        0.067641

BFGS:   41 23:07:11    -1077.366698        0.058106

BFGS:   42 23:07:11    -1077.367796        0.060969

BFGS:   43 23:07:11    -1077.368842        0.069386

BFGS:   44 23:07:12    -1077.370096        0.076307

BFGS:   45 23:07:12    -1077.371267        0.048851
Energy of re-relaxed empty MOF: -1077.371 eV

The MOF returns to its original empty reference energy upon re-relaxation, confirming that this deformation is physically relevant and is induced by the adsorbate molecule. In Case #3, this re-relaxed energy will be more negative (more favorable) than the original empty MOF relaxation. Thus, we take the reference empty MOF energy ( $E_{\mathrm{MOF}}$ in Eqn. 1) to be the minimum of the original empty MOF energy and the re-relaxed MOf energy:

E_mof = min(E_mof_empty, E_mof_rerelax)

# get adsorbate reference energy
h2o = mof_h2o[-3:]
h2o.calc = calc
E_h2o = h2o.get_potential_energy()

# compute adsorption energy
E_ads = E_combo - E_mof - E_h2o
print(f"Adsorption energy of H2O in WOBHEB_0.11_0: {E_ads:.3f} eV")

Adsorption energy of H2O in WOBHEB_0.11_0: -0.686 eV

This adsorption energy closely matches that from DFT (–0.699 eV) [1]. The strong adsorption energy is a consequence of both H₂O chemisorption and MOF deformation. We can decompose the adsorption energy into contributions from these two factors. Assuming rigid H₂O molecules, we define $E_{\mathrm{int}}$ and $E_{\mathrm{MOF,deform}}$ , respectively, as

E_{\mathrm{int}} = E_{\mathrm{MOF+H2O}}(r_{\mathrm{MOF+H2O}}) - E_{\mathrm{MOF}}(r_{\mathrm{MOF+H2O}}) - E_{\mathrm{H2O}}(r_{\mathrm{MOF+H2O}}) \tag{2}

(2)

E_{\mathrm{MOF,deform}} = E_{\mathrm{MOF}}(r_{\mathrm{MOF+H2O}}) - E_{\mathrm{MOF}}(r_{\mathrm{MOF}}) \tag{3}

(3)

$E_{\mathrm{int}}$ describes host host–guest interactions for the MOF in the adsorbed state only. $E_{\mathrm{MOF,deform}}$ quantifies the magnitude of deformation between the MOF in the adsorbed state and the most energetically favorable empty MOF geometry determined from the workflow presented here. It can be shown that

E_{\mathrm{ads}} = E_{\mathrm{int}} + E_{\mathrm{MOF,deform}} \tag{4}

(4)

For H₂O adsorption in WOBHEB_0.11, we have

E_int = E_combo - E_mof_adsorbed_state - E_h2o
print(f"E_int: {E_int}")

E_int: -0.9692270755765957

E_mof_deform = E_mof_adsorbed_state - E_mof_empty
print(f"E_mof_deform: {E_mof_deform}")

E_mof_deform: 0.2831425666809082

E_ads = E_int + E_mof_deform
print(f"E_ads: {E_ads}")

E_ads: -0.6860845088956875

$E_{\mathrm{int}}$ is equivalent to $E_{\mathrm{ads}}$ when the MOF is assumed to be rigid. In this case, failure to consider adsorbate-induced deformation would result in an overestimation of the adsorption energy magnitude.

Acknowledgements & Authors¶

Logan Brabson and Sihoon Choi (Georgia Tech) and the OpenDAC project.

References¶

Sriram, A., Choi, S., Yu, X., Brabson, L. M., Das, A., Ulissi, Z., Uyttendaele, M., Medford, A. J., & Sholl, D. S. (2024). The Open DAC 2023 Dataset and Challenges for Sorbent Discovery in Direct Air Capture. ACS Central Science, 10(5), 923–941. 10.1021/acscentsci.3c01629
Queen, W. L., Hudson, M. R., Bloch, E. D., Mason, J. A., Gonzalez, M. I., Lee, J. S., Gygi, D., Howe, J. D., Lee, K., Darwish, T. A., James, M., Peterson, V. K., Teat, S. J., Smit, B., Neaton, J. B., Long, J. R., & Brown, C. M. (2014). Comprehensive study of carbon dioxide adsorption in the metal–organic frameworks M2(dobdc) (M = Mg, Mn, Fe, Co, Ni, Cu, Zn). Chem. Sci., 5(12), 4569–4581. 10.1039/c4sc02064b
Yu, D., Yazaydin, A. O., Lane, J. R., Dietzel, P. D. C., & Snurr, R. Q. (2013). A combined experimental and quantum chemical study of CO2 adsorption in the metal–organic framework CPO-27 with different metals. Chemical Science, 4(9), 3544. 10.1039/c3sc51319j
Alonso, G., Bahamon, D., Keshavarz, F., Giménez, X., Gamallo, P., & Sayós, R. (2018). Density Functional Theory-Based Adsorption Isotherms for Pure and Flue Gas Mixtures on Mg-MOF-74. Application in CO2 Capture Swing Adsorption Processes. The Journal of Physical Chemistry C, 122(7), 3945–3957. 10.1021/acs.jpcc.8b00938
Witman, M., Ling, S., Jawahery, S., Boyd, P. G., Haranczyk, M., Slater, B., & Smit, B. (2017). The Influence of Intrinsic Framework Flexibility on Adsorption in Nanoporous Materials. Journal of the American Chemical Society, 139(15), 5547–5557. 10.1021/jacs.7b01688

Loading Pre-trained Models¶

Adsorption in rigid MOFs: CO2 Adsorption Energy in Mg-MOF-74¶

Adsorption in flexible MOFs¶

H2O Adsorption Energy in Flexible WOBHEB with UMA¶

Acknowledgements & Authors¶

Adsorption in rigid MOFs: CO₂ Adsorption Energy in Mg-MOF-74¶

H₂O Adsorption Energy in Flexible WOBHEB with UMA¶